Optimize something:
Contents
Updates
- 2017-01-26 submission process updated -- only one t-square project to submit to.
- 2017-08-31 Optimization criteria changed from max Sharpe to min vol.
Overview
In this project you will use what you learned about optimizers to optimize a portfolio. That means that you will find how much of a portfolio's funds should be allocated to each stock so as to optimize it's performance. We can optimize for many different metrics. In previous versions of this assignment, we tried to maximize Sharpe Ratio. We're changing it this time to define "optimal" as minimum volatility.
You will leverage the functions you created in the last project that assessed the value of a portfolio with a given set of allocations.
An older version of this project: MC1-Project-2-archive
Task
Implement a Python function named optimize_portfolio() in the file optimization.py that can find the optimal allocations for a given set of stocks. You should optimize for minimum volatility (i.e., standard deviation of daily return).
The function should accept as input a list of symbols as well as start and end dates and return a list of floats (as a one-dimensional numpy array) that represents the allocations to each of the equities. You should take advantage of routines developed in the portfolio analysis project to compute daily portfolio value and statistics. You should cut-and-paste your code for the functions that did this from the last project into optimization.py.
You are given the following inputs for optimizing a portfolio:
- A date range to select the historical data to use (specified by a start and end date)
- Symbols for equities (e.g., GOOG, AAPL, GLD, XOM). Note: You should support any symbol in the data directory.
Your goal is to find allocations to the symbols that maximize Sharpe ratio. Assume 252 trading days in a year and a risk free return of 0.0 per day. You should implement the following API EXACTLY, if you do not your submission will be penalized.
import datetime as dt
allocs, cr, adr, sddr, sr = \
optimize_portfolio(sd=dt.datetime(2008,1,1), ed=dt.datetime(2009,1,1), \
syms=['GOOG','AAPL','GLD','XOM'], gen_plot=False)
Where the returned output is:
- allocs: A 1-d Numpy ndarray of allocations to the stocks. All the allocations must be between 0.0 and 1.0 and they must sum to 1.0.
- cr: Cumulative return
- adr: Average daily return
- sddr: Standard deviation of daily return
- sr: Sharpe ratio
The input parameters are:
- sd: A datetime object that represents the start date
- ed: A datetime object that represents the end date
- syms: A list of symbols that make up the portfolio (note that your code should support any symbol in the data directory)
- gen_plot: If True, create a plot named plot.png
ALL of your code should be present in the single file optimization.py
Template
Instructions:
- Ensure your directory structure has been properly checked out from github.
- Implement the optimize_portfolio() function in optimize_something/optimization.py.
- To execute, run python optimization.py from the optimize_something/ directory.
Your solution to the optimization problem should leverage the software you developed in the last assignment. However you cannot call your old file analysis.py, you must copy and paste that old code into the single file for this assignment. To test your code, we will be calling optimize_portfolio() only. Make sure the output and plot look like the examples shown below.
Suggestions
- Refer to comments in the provided helper code for pointers regarding how to implement it. In order to specify bounds and constraints when using the scipy.optmize module, you'll need to use a special syntax explained here: http://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.minimize.html
- For bounds, you simply need to pass in a sequence of 2-tuples (<low>, <high>). Just remember that you need to supply as many tuples as the number of stocks in your portfolio.
- For constraints, it's a little tricky. You need to pass in a sequence of dicts (dictionaries), one dictionary per constraint. Each dictionary must specify the type of constraint ('eq' for equality, or 'ineq' for inequality), and a function that returns 0 only when the input satisfies the constraint (this is the same input that is supplied to your evaluation function). E.g. to constrain the sum of all values in the input array to be less than 50, you could pass in the following (lambdas are just anonymous functions defined on-the-spot):
constraints = ({ 'type': 'ineq', 'fun': lambda inputs: 50.0 - np.sum(inputs) })
- Use a uniform allocation of 1/n to each of the n assets as your initial guess.
Example output 1
Here's an example output for your function. These are actual correct values that you can use to check your work.
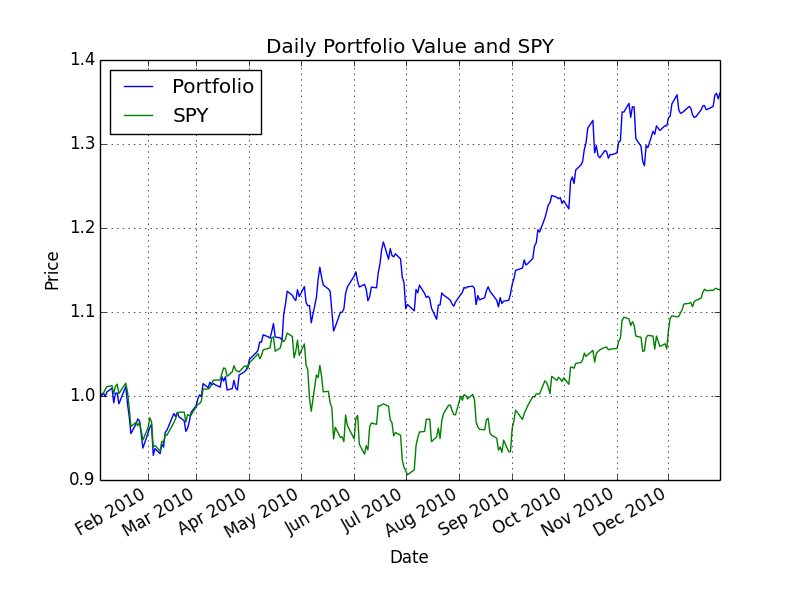
Start Date: 2010-01-01 End Date: 2010-12-31 Symbols: ['GOOG', 'AAPL', 'GLD', 'XOM'] Optimal allocations: [ 5.38105153e-16 3.96661695e-01 6.03338305e-01 -5.42000166e-17] Sharpe Ratio: 2.00401501102 Volatility (stdev of daily returns): 0.0101163831312 Average Daily Return: 0.00127710312803 Cumulative Return: 0.360090826885
Corresponding comparison plot:
Example output 2
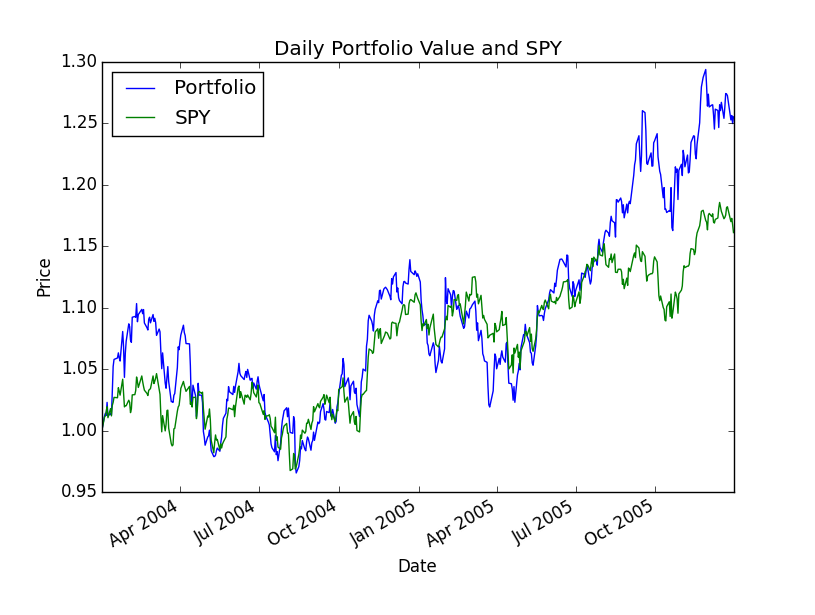
Start Date: 2004-01-01 End Date: 2006-01-01 Symbols: ['AXP', 'HPQ', 'IBM', 'HNZ'] Optimal allocations: [ 7.75113042e-01 2.24886958e-01 -1.18394877e-16 -7.75204553e-17] Sharpe Ratio: 0.842697383626 Volatility (stdev of daily returns): 0.0093236393828 Average Daily Return: 0.000494944887734 Cumulative Return: 0.255021425162
Example output 3
Start Date: 2004-12-01 End Date: 2006-05-31 Symbols: ['YHOO', 'XOM', 'GLD', 'HNZ'] Optimal allocations: [ -3.84053467e-17 7.52817663e-02 5.85249656e-01 3.39468578e-01] Sharpe Ratio: 1.5178365773 Volatility (stdev of daily returns): 0.00797126844855 Average Daily Return: 0.000762170576913 Cumulative Return: 0.315973959221
Example output 4
Start Date: 2005-12-01 End Date: 2006-05-31 Symbols: ['YHOO', 'HPQ', 'GLD', 'HNZ'] Optimal allocations: [ -1.67414005e-15 1.01227499e-01 2.46926722e-01 6.51845779e-01] Sharpe Ratio: 3.2334265871 Volatility (stdev of daily returns): 0.00842416845541 Average Daily Return: 0.00171589132005 Cumulative Return: 0.229471589743
Minor differences in float values may arise due to different implementations.
What to turn in
Be sure to follow these instructions exactly!
Via T-Square, submit as attachments (no zip files; refer to schedule for deadline):
- Your code as optimization.py (only the function optimize_portfolio() will be tested). Make sure that all necessary code is in that file.
- A report report.pdf that includes a chart comparing the optimal portfolio with SPY as using the following parameters:
Start Date: 2008-06-01, End Date: 2009-06-01, Symbols: ['IBM', 'X', 'GLD']
Unlimited resubmissions are allowed up to the deadline for the project.
Rubric
Part 1: Chart is correct [20 points]
- -20 no chart or chart is total nonsense
- -10 chart wrong shape (incl. wrong time period, etc) xor -5 chart partly wrong shape (diverges from correct halfway through, etc)
- -10 chart not normalized xor -5 chart data scale substantially wrong (right shape, normalized to 1, but max/end values wrong, 3.5 instead of 2.5 etc)
- -10 missing required data series (didn’t plot one of portfolio or SPY)
- -2 chart labels/text unreadable (too small, labels overlap a lot, etc)
- Min score: 0.
Part 2: 10 test cases [80 points]
We will test your code against 10 cases (8 points per case). Each case will be deemed "correct" if:
- sum(allocations) = 1.0 +- 0.02 (2 points)
- Each allocation is between 0 and 1.0 +- 0.02 (negative allocations are allowed if they are very small) (2 points)
- Each allocation matches reference solution +- 0.10 (4 points)
Required, Allowed & Prohibited
Required:
- Your project must be coded in Python 2.7.x.
- Your code must run on one of the university-provided computers (e.g. buffet02.cc.gatech.edu).
- Use the code for reading in historical data provided in util.py
- Your code must run in less than 5 seconds on one of the university-provided computers.
Allowed:
- You can develop your code on your personal machine, but it must also run successfully on one of the university provided machines or virtual images.
- Your code may use standard Python libraries (except os).
- You may use the NumPy, SciPy, matplotlib and Pandas libraries. Be sure you are using the correct versions.
- You may reuse sections of code (up to 5 lines) that you collected from other students or the internet.
- Code provided by the instructor, or allowed by the instructor to be shared.
Prohibited:
- Any use of global variables.
- Any libraries not listed in the "allowed" section above.
- Calls to code in any other local files besides util.py (e.g. don't depend on analysis.py being present).
- Use of any code other than util.py to read in data.
- Use of Python's os module.
- Any code you did not write yourself (except for the 5 line rule in the "allowed" section).
- Camels and other dromedaries.