MC1-Project-2

Overview

In this project you will use what you learned about optimizers to optimize a portfolio. That means that you will find how much of a portfolio's funds should be allocated to each stock so as to optimize it's performance. In this case we define "optimal" as maximum Sharpe ratio.

You will leverage the functions you created in the last project that assessed the value of a portfolio with a given set of allocations.

Task

Implement a Python function named find_optimal_allocations() that can find the optimal allocations for a given stock portfolio. You should optimize for Sharpe ratio.

The function should accept as input historical stock prices (supplied as a pandas dataframe, with each column representing one equity), and return a list of floats (as a one-dimensional numpy array) that represents the allocations to each of the equities. Use functions developed in the portfolio analysis project to compute daily portfolio value and statistics.

Template

Instructions:

• Download mc1_p2.zip, unzip inside ml4t/
• Copy analysis.py (your solution for MC1-Project-1) to mc1_p2/portfolio/.
• Implement the find_optimal_allocations() function in mc1_p2/portfolio/optimization.py.
• To execute, run python -m portfolio.optimization from mc1_p2/ directory.

A helper function (optimize_portfolio) has been included in the template code (see mc1_p2/portfolio/optimization.py), which is called with the desired date range and symbols (see test_run()):

start_date = '2010-01-01'
end_date = '2010-12-31'
symbols = ['GOOG', 'AAPL', 'GLD', 'XOM']
optimize_portfolio(start_date, end_date, symbols)

This in turn reads stock price data, and calls the function to find optimal allocations (you need to implement this):

allocs = find_optimal_allocations(prices)

Your solution to the optimization problem should leverage the function you wrote assess_portfolio() that you submitted as part of analysis.py in the last assignment. Note that when your code is submitted for this project, you will not be submitting your analysis.py code, but instead your code will be calling our implementation of that. Accordingly, be sure you've implemented the API to assess_portfolio() correctly!

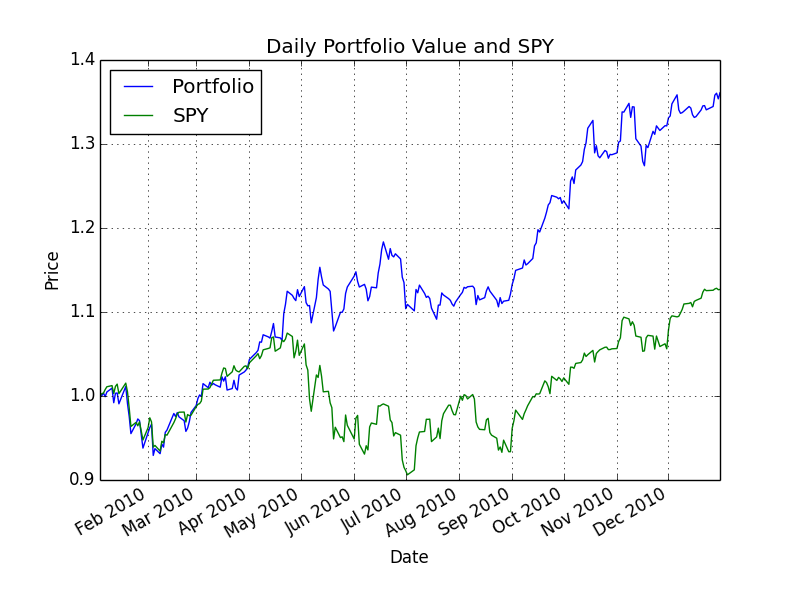
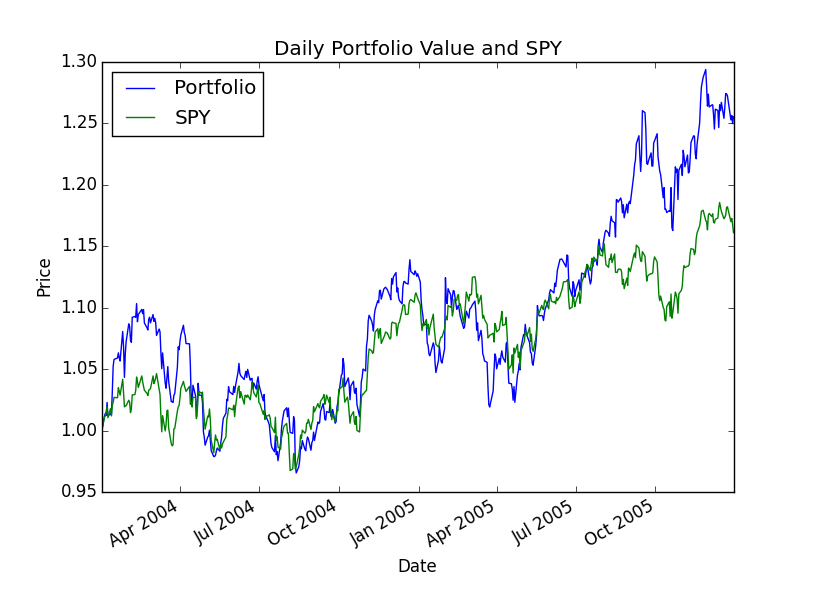
The helper function (optimize_portfolio()) prints out the optimal allocations, and some statistics. It also plots a chart comparing the daily value of your portfolio over the year and compares it to SPY. The portfolio and SPY are normalized to 1.0 at the beginning of the period.

Make sure the output and plot look like the examples shown below.

Suggestions

Refer to comments in find_optimal_allocations() for pointers regarding how to implement it. In order to specify bounds and constraints when using the scipy.optmize module, you'll need to use a special syntax explained here: http://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.minimize.html

For bounds, you simply need to pass in a sequence of 2-tuples (<low>, <high>). Just remember that you need to supply as many tuples as the number of stocks in your portfolio.

For constraints, it's a little tricky. You need to pass in a sequence of dicts (dictionaries), one dictionary per constraint. Each dictionary must specify the type of constraint ('eq' for equality, or 'ineq' for inequality), and a function that returns 0 only when the input satisfies the constraint (this is the same input that is supplied to your evaluation function). E.g. to constrain the sum of all values in the input array to be less than 50, you could pass in the following (lambdas are just anonymous functions defined on-the-spot):

constraints = ({ 'type': 'eq', 'fun': lambda inputs: 50.0 - np.sum(inputs) })

Example output 1

Here's an example output for your function. These are actual correct values that you can use to check your work.

Start Date: 2010-01-01
End Date: 2010-12-31
Symbols: ['GOOG', 'AAPL', 'GLD', 'XOM']
Optimal allocations: [  5.38105153e-16   3.96661695e-01   6.03338305e-01  -5.42000166e-17]
Sharpe Ratio: 2.00401501102
Volatility (stdev of daily returns): 0.0101163831312
Average Daily Return: 0.00127710312803
Cumulative Return: 0.360090826885

Corresponding comparison plot:

Example output 2

Start Date: 2004-01-01
End Date: 2006-01-01
Symbols: ['AXP', 'HPQ', 'IBM', 'HNZ']
Optimal allocations: [  7.75113042e-01   2.24886958e-01  -1.18394877e-16  -7.75204553e-17]
Sharpe Ratio: 0.842697383626
Volatility (stdev of daily returns): 0.0093236393828
Average Daily Return: 0.000494944887734
Cumulative Return: 0.255021425162

Minor differences in float values may arise due to different implementations.

What to turn in

Be sure to follow these instructions diligently!

Via T-Square, submit as attachments (no zip files; refer to schedule for deadline):

• Your code as optimization.py (only the function find_optimal_allocations() will be tested)
• Plot comparing the optimal portfolio with SPY as comparison_optimal.png using the following parameters:
  Start Date: 2010-01-01, End Date: 2010-12-31, Symbols: ['GOOG', 'AAPL', 'GLD', 'HNZ']

Unlimited resubmissions are allowed up to the deadline for the project.

Rubric

We will test your code against 10 cases. Each case will be deemed "correct" if:

• sum(allocations) = 1.0 +- 2%
• sum(abs(allocations)) = 1.0 +- 2%
• Each allocation is between 0 and 1.0 +- 1% (negative allocations are allowed if they are very small)
• Each allocation matches reference solution +- 10%